Equivalent Fractions are Weird

24 Apr Equivalent Fractions are Weird

Recently, I had the pleasure of being a part of several equivalent fraction lessons in 3^rd and 4^th grades.  From California to Minnesota, to Colorado—and everywhere in between, I encourage teachers and students to have the same conversation: equivalent fractions are weird.

And they are, aren’t they?  I mean, if you are an English language learner, or maybe just a student who is struggling with abstract concepts, equivalent fractions might be the weirdest thing you’ve encountered in mathematics class.  If you are a primary teacher and do not dabble in much fraction work, hang out with me, this still applies to you.  The idea of the equal sign being ‘the same as’ and not ‘the answer’ or the ‘total’ starts with you all.  What we teach in K-2 regarding the equal sign plays out in the subsequent 8 grades.

2=2, right? I mean, 2 is equivalent to 2.  As we develop an understanding of the equal sign starting in kindergarten, we teach students this pre-algebraic idea that the equal sign means ‘the same as’.  From an EL perspective, the equal sign makes sense when referring to quantities.  2 looks like the other 2, it is the same quantity as the other 2, of course, they are the ‘same.’

What begins to happen here is our over-emphasis of the word, same.  For many students, the same begins to mean looks and is the same—it’s congruent.  But really, we could mean the same in terms of looks, but what we really mean is the same quantity or the same amount.

So, when I am teaching, I post this on the board:

2 = 2

Me: “Class, do you agree that these are equivalent?”

Class: “Yes.”

Me: “Why?” (My favorite question, even when I think they get it, I often find what comes out next is not at all what I am expecting).

Class: “Because they are the same!”

Me: “Tell me more.” (Again, I agree they are the same, but I know we have different interpretations of the same.”

Class:  “Well, they are just the same.  You just have two of them.”

Ahhh… and now I understand what they mean by same and it is NOT my definition.

Me: “So class, I can see that these two look the same and you are telling me they are the same, because 2 is well, 2. But can anyone tell me then why you think ½ = 4/8 ?  Why are you telling me ½ is equivalent to 4/8? “

Class: “Because they are the same!!”

Me: “Ummmmm, they are?”  “Who can tell me why this is weird?”

I must poke and prod the class a little for them to start to see that this is indeed WEIRD.  Finally, I get a student who also happens to be EL and happens to be the student the teacher told me was struggling with this concept.  He says, “It’s weird because they don’t look the same. They don’t have the same numbers.”

Ahhhhh.  And there we have it.  Why isn’t anyone else questioning this?  Why are students just believing us when we tell them they are the same?  Why aren’t we questioning them on their definitions of the same? I worked with several classrooms on this idea as they explored the concept of equivalent fractions and what I felt was missing in nearly all of them was a conversation around the weirdness of saying ½ is equivalent to 4/8.  I want my kids thinking, “Ummm… teacher, you’ve lost your mind, or maybe you’ve gone blind.”  But instead, our children begin to just go with it. If the teacher says it, it must be true.

Next, I begin to challenge them to PROVE that they are the same and not because they look the same. They must be the same in a different way for us to call them equivalent.  Students have their paper fraction strips out and begin to investigate.

Students begin to describe to me that when the fractions line up, that means they are equivalent.  The ½ line lines up with 4/8ths when comparing the wholes and therefore, they are equivalent.

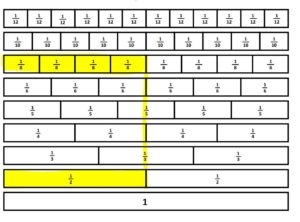
Get it? Good… start your worksheet.

WHOA.  Hold your horses. Keep going and you are bound to encounter many students who can line up fractions but who continue to struggle with the real meaning of equivalence.

As I recently taught this lesson, I asked students how they KNEW the two fractions were equivalent.  Students became impassioned as they tried to get their partners and me to understand it’s because they’re lined up!!!

Me: “So, you’re telling me that ½ = 4/8 because they line up?”

Class” Yes.”

Me: “Why do you think that?”

Students become insistent on showing me what they mean by lining up.  I love these moments.  The moments in which students are owning learning, determined, passionate, and willing to fight for what they think.  I play devils advocate a bit more and really push back on them.

Me: “Yes, but how do you know they are equivalent? What if I misalign them, are you telling me they are no longer equivalent?”

Class, “Correct.  You have to line them up right to see that they match.”

Facepalm (but on the outside, my neutral face stays intact). And here lies the second issue with equivalent fractions.

I now must follow the next line of thinking they’ve thrown out.  At the surface, they get it, but as I question them I realize they are abiding by the ‘rules’ or structures they’ve learned for proving—just line them up, but be careful how you line up!

Me: “Ok, let’s explore that idea.  By folding or cutting, prove to me—other than lining up, that ½ is equivalent to 4/8.”

(I really must push EVERY class on this one.  They try to explain what they’re thinking, but they really struggle to prove it.  Finally, I get a few students who begin to stack the fraction strips on top of one another.)

Me: “So are those equivalent?”

Students: “Yes!”

Me: “How do you know?”

Students: “Because there isn’t anything left over.”

WOOT. We are getting there, but I don’t want to take it at face value.  They need to say more.

Me: “Tell me more, what do you mean there isn’t anything left over?”

Students: “Look, they line up perfectly, so that means they are the same.”

Me: “Class, try  ____’s way.  See if you can prove that they are the ‘same.”

Students do so and begin to develop a new language around equivalence.  We explore that what they really mean is the fractions take up the same amount of space—they are equivalent.  They have the same ‘area.’

So, I go back to my question, “So, are they equivalent because they line up?”

Student: “Well, no, they line up AND they look the same.”

Me: “So they still look the same? Tell me more. “(Gosh, I LOVE that prompt.)

Student” “Yes, they look like the same amount and if you line them up you can prove it.”

Me: “I agree. I can prove it if I line them up, but I ‘d argue they are equivalent when they aren’t lined up too.”

Student: “Yes, because even if they don’t line up, their space didn’t change.  It’s easier to see that they are the same space when we line them up, but even if they’re not lined up, they are still equivalent!  We would have to measure them or stack them to prove it.”

Ahhhh… I love these moments.  It’s a good thing this kid was so eloquent, but what about everyone else’s thoughts?  Did they just check out because he started talking?  I don’t know if EVERYONE is catching on, so I make them all prove it.

Me: “Friends, with your partners, prove that if we line up two fractions and they are ‘inline’ with each other that they are equivalent. Then explain why they are equivalent, even if we don’t line them up.”

Students begin to work feverishly cutting, folding, measuring, to prove that even when they aren’t lined up, they are still equivalent.

They have the same space.

They have the same area.

It is the same amount.

Me: “So, then why is this weird that 2= 2 and ½ = 4/8?”  The class debriefs that ½ and 4/8 are just the names of the same amount of space. So, equivalence doesn’t always have to do with how it looks.  We explore what 2 is (two objects and the numeral is just the name for that quantity).

I leave the rooms planting one more big question to see if their understanding can take them to the next level, “So, here is 1/3 and here is 1/3.”

Are they equivalent?  The whole rectangles are the same size.  Kids have initial reactions, some instantly say no, arguing they aren’t the same.  Others counter-argue and remind their peers that just because they don’t look the same doesn’t mean they aren’t EQUIVALENT.

On to tomorrow where I will make them prove this idea again!

It’s not about fractions lining up. I love a number line as much as the next math girl. I love fraction resource pages that show us the fractions all lined up as a tool.  These are great ADDITIONAL ways to show equivalence, but we must push through to ensure students truly understand equivalence.

It’s not about multiplying the top (numerator) and bottom (denominator). (This, of course, works to generate equivalent fractions, but next, we must investigate WHY it works— another reason paper fractions are one of my favorite fraction tools.  They allow us to fold, double, etc. to prove equivalence.  Folding allows us to see why multiplying impacts both the numerator and the denominator.

It’s about language and taking it literally to help our EL’s, but it’s also about taking it abstractly with the support of visuals.  It’s about having honest conversations around things we think are ‘weird’ and allowing that feeling to be valid in the math classroom.  We say a whole lot of things that seem contradictory to a sense-making language learner.  This conversation will continue as soon as we explore the relevance of anchor charts and language t-charts.  Do you see how a t-chart could help in this lesson?  One side labeled equivalent whole numbers with examples and pictures.  The other side, equivalent fractions, with fractions and pictures.  These types of charts allow students to compare, contrast, and make connections.  This idea has now been repeated multiple times in so many lessons since then.  As we discuss measurement conversations 1000mL = 1 L. Are you crazy?  1000 is NOT the same as 1??!  These types of experiences allow students to think deeply amount how and why we can say a statement such as 1000mL = 1L and how we need to truly understand the concepts before teaching tricks, shortcuts, etc.  Otherwise, we are fostering the idea that math doesn’t make sense and therefore we need ‘tricks’ to solve problems.

Can you see some real-world connections here?

If I add a ½ cup of flour to Sara’s cookies, but only 4/8’s cup flour to John’s, will the cookies turn out the same?  Looks sure are deceiving.

My friends.  Do you feel inspired and empowered to bring more sense making to your classroom?  Are you ready to go BE GREAT?  I know you can do it.  Diving deeper and creating meaning takes more time, but with time spent on depth, we gain time as the units go on.  Have confidence and honor these REAL and WEIRD conversations in your mathematics classrooms.

Help me continue the conversation online.  Tweet your responses @sekiebler