09 Sep Alligators Eat Bigger Numbers? Butterflies Work with Fractions?

I have taught about alligators eating bigger numbers for years.  It’s a great visual.  The comparisons symbols ‘look’ like alligator mouths.  Add some teeth and voila!  Kids can tell which number is bigger because the mouth of the alligator opens to the bigger number…..totally harmless, right?

This is one of those ‘fun’ ideas I truly felt was helping my students.  It’s one of the many things I’ve since learned may not be as helpful as I thought.   They are alligators, how harmful could they be? Uggghhhh just that question alone should have you second-guessing their use in the math classroom.

They are not as harmful as the real deal in U.S. swamps, but in terms of mathematical understanding, they aren’t really helping student understanding.

When we say that 34 is greater than 29, we want students to truly understand the comparison.  We want students to know:

• 34 is three tens and four ones and 29 is two tens and nine ones.  Therefore 34 has more tens, making it GREATER.
• 34 is farther on the number line than 29.  29 is LESS than 34 because it is not as ‘far’ on the number line. It takes less to get to 29 than to 34.  Even more specifically, when using a benchmark number such as 50, we know 34 is closer to 50 and 29 is less close.
• 34 ones are more (or greater) than 29 ones.
• In relation to area, 34 sq units take up more space than 29 square units.
• How to read the equality/inequality statement  34 > 29  (34 is greater than 29)  and 29< 34 (29 is less than 34).

Although the first three/four require good conceptual understanding and many opportunities to build, draw, and compare numbers, and can then use the ‘alligator’ to help remember the symbol, it is the fourth bullet that the alligator begins to cause harm.

Our middle and high school teachers are telling us our students come to them only being able to explain if the bigger number is being eaten, but they aren’t able to read and understand equality and inequality statements.   This begins to impact future mathematics in algebra and beyond.    Students need to accurately read these statements.

When we use worksheets such as this:

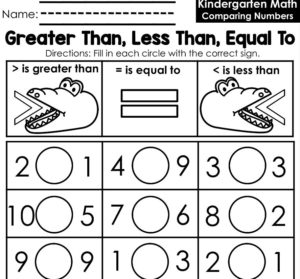
We are making matters worse.  Students are drawing lots of ‘mouths’ but never really stating the inequality or equality statement.

Here are some solutions, as I don’t believe we should throw everything out the window.  I’m not a fan of the extreme mathematics teachers who can’t see how things like alligators do help students remember which sign is which. The alligator (greater than, less than symbol) is a convention of mathematics. It’s most important students understand the concept first, then do what is needed to understand the conventions.

I agree alligator mouths aren’t the best conceptual way to teach this skill, but I’m also a true elementary teacher who likes fun cute things.  I just want to be sure that I’m accompanying the ‘cute’ with good teaching that doesn’t teach kids tricks for the sake of cute and instead uses the cute to support the deep conceptual learning and rich math language in the classroom.  So, I don’t think it has to be one or the other, I just think we need to look at what we are doing and ensure we aren’t robbing students of true understanding.  Here are some ideas to help maintain strong understanding:

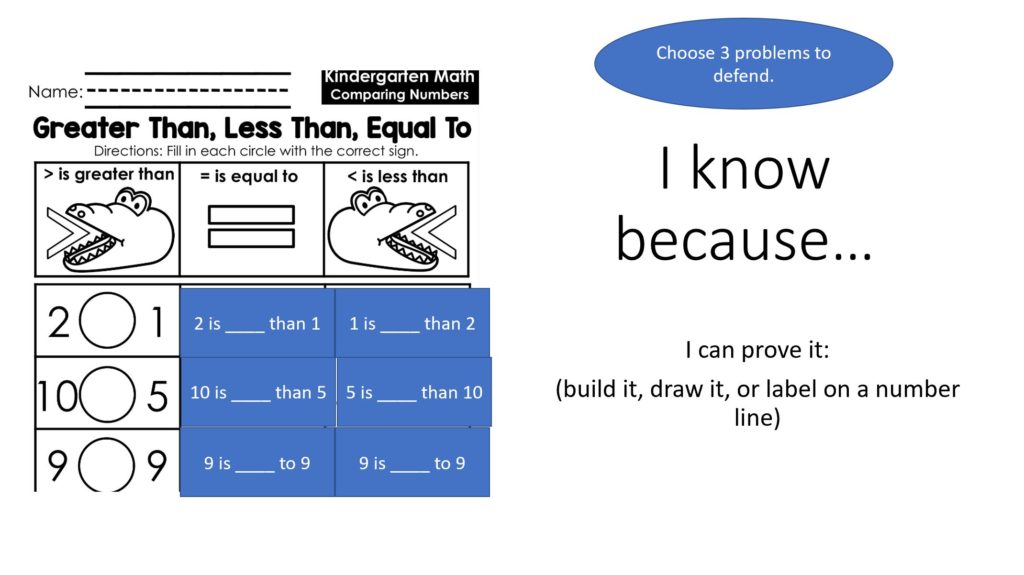
• If we continue to use alligators, we need to ensure we are also practicing the correct reading of the equality and inequality statements.  Students should be able to practice saying the statements both ways:  29 is less than 34 and 34 is greater than 29.  We shouldn’t be drawing the alligator mouths and never practice using the language and actually ‘reading’ the sign.  Maybe we could transform that worksheet into something like this where students have to place the words in the blanks, read aloud, and then choose a few to defend.

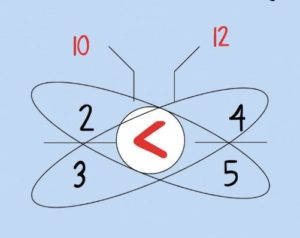
• Try the number line method.  If we were comparing the number 34 and 29, we could find them first on a number line.  The lesser number will be closest to the beginning of the number line which also happens to look like the less than symbol. The 34 is further on the number line, closest to the greater than sign of the number line.  This is a good visual to help them remember which symbol is which and doesn’t perpetuate the ‘alligators in math class, so math is just a trick’ notion.  This method not only emphasizes the conceptual part of comparing numbers but also gives students a way to remember the symbols.  This method will help students as they move into decimals and fractions as it will also allow them to compare numbers by using the visual of a number line with benchmark numbers.

• Try the dot method.  Why didn’t I learn this as a kid?  I almost lost my mind when I heard this one.  I’ve used it with students now and it is SO effective.  Students place two dots (vertically) next to the number that is greater.  They then place one dot next to the number that is less.  Finally, they connect the dots.  This will always make the correct symbol AND it reinforces which number is greater/less than.  With this method, you still need to practice READING the inequality statement, but the dots should help students with this reading.

• Here is another FANTASTIC visual idea from @berkelyeverett.  You should definitely be following his visuals 

And of course, no matter the method we use, it should always be accompanied by many opportunities to prove, draw, build, discuss and rehearse.  Students need many opportunities to defend HOW they know one number is greater and one number is less.   I’ve used only digit numbers above, seemingly simple, but these same strategies apply to larger numbers.  Let’s be wary of just looking at each digit and comparing.  Ensure students understand not just each ‘place’ but the value of those places and the value of the entire number.  Using quantity drawings helps students to understand the magnitude of a number.  Students who lack number sense don’t really have an idea of how much or how big a number is, making comparisons very difficult or reliant solely on tricks.

Quantity Drawing

This is also true for quantities such as 2/5 and 4/8.  Students must understand how much ‘space’ each of those fractions takes up in order to compare them.  If they use number lines, they should know how far on a number line they fall because they also understand benchmark numbers or fractions to help (see second bullet above). The alligators help remember the symbols, but upper-grade teachers are perpetuating misunderstanding by having students use the butterfly method to determine the greater number.   Essentially, you multiply diagonally and the greater number wins 🙂 Oh please!  No butterflies until students have many other opportunities to compare numbers using methods that build conceptual understanding.  I want them to be able to reason, draw, relate to benchmarks, create equivalent fractions, etc. before they fully rely on a cool trick like the butterfly method.

• 2/5 is less than 4/8 because 2/5 isn’t quite half and 4/8 is equivalent to half. I can use benchmark fractions to understand this.
• 4/8 is farther on the number line than 2/5. I can draw two number lines. One with fifths, one with 8ths, and then I can compare.

• I can use fraction strips to reason.

• I can create equivalent fractions  2/5 = 16/40 and 4/8 = 20/40.  16/40 < 20/40

Remember, it’s a trick.

Our goal isn’t to foster magic in our classrooms, we are fostering mathematics.

We aren’t training magicians.

We are training mathematicians.

Magicians can make you think you understand something that you don’t.

Magicians are ultimately trying to deceive you.

Mathematicians can reason, defend, prove, etc.  Mathematicians are trying to make the learning EVIDENT.  Mathematics makes sense.

Let’s teach sense-making first, cute rhymes, tricks, pictures, and methods LAST.

To keep a method, trick, picture, rhyme, ask yourself:

• Does this method I’m teaching help students to understand the math or does it give a false sense of understanding?
• Can this method or trick be explained mathematically as to WHY it works?
• Does this method or trick impede precise language or conceptual understanding?
• Does this method emphasize speed or completion over understanding “they don’t get it, but they can do it.”

If you said yes to any of the above.  Spend more time building the concept FIRST and prior to introducing any shortcut or a cute way of remembering.

What do you think?  How is this learning impacting your own understanding and/or your teaching methods?  I’d love to continue the conversation.